Partie cours : réfraction et dispersion

<< retour




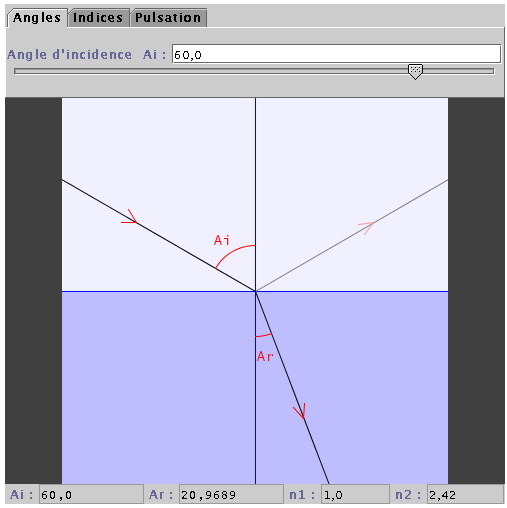
Présentation générale de l'applet :

L'idée de ce programme est de simuler le  trajet d'un rayon lumineux, à la traversée d'un milieu vers un autre. Les phénomènes de reflexion et de réfraction seront étudiés par cette occasion.

Sur l'applet ci-dessus, on distingue les deux milieux différents : le premier correspondant à la partie supérieure ( bleu clair ), et le second correspondant à la partie inférieure ( bleu fonçé ).

Le rayon va donc subir à la fois une réflexion, et une réfraction, ce qui apparaît bien sur le dessin.

L'utilisateur peu choisir le milieu 1, le milieu 2, caractérisés par leur indice optique, à partir duquel se porte le calcul de la direction des rayons lumineux.

Pour une meilleure simulation, on peut choisir le type de lumière émise, qui a une longueur d'onde bien définie, et qui donne la pulsation.

Rappels des lois physiques

La réflexion

Quand un rayon lumineux arrive à la surface d'un milieu avec un angle d'incidence Ai par rapport à la normale, il est réfléchi avec le même angle.

La réfraction

Quand un rayon lumineux arrive sur une discontinuité, c'est à dire à la limite de deux milieux différents, il va y avoir phénomène de réfraction pour certaines valeur de l'angle d'incidence, en fonction des indices des milieux.

SI l'angle d'incidence est Ai par rapport à la normale, alors le rayon réfracté aura un angle Ar par rapport à la normale, et il existe une relation qui lie ces deux angles en fonction des indices respectifs des milieux en question, qui nous est donnée par le Loi de Descartes :

Relation de Snell-Descartes :
Soit N1 l'indice du milieu 1, N2 l'indice du milieu 2, on a : N1.sin(Ai) = N2.sin(Ar)

Notion d'angle limite

De la relation de Descartes, on a : sin(Ar) = N1/N2.sin(Ai)
Il apparaît donc clairement qu'il y aura réfraction tant que  sin(Ar) <= 1, c'est à dire pour un angle d'incidence vérifiant sin(Ai) <= N2/N1
Au delà de cet angle limite, il y a alors phénomène de reflexion totale, c'est à dire que la toalité du rayon incident est réflechi.

Phénomène de dispersion

Le phénomène de dispersion traduit une réalité observée par Snell, quand à la variaton de l'indice optique d'un milieu en foncion de la longeur d'onde de la lumière émise.

En effet, soit No l'indice propre du milieu, il convient d'utiliser dans les calculs N(lambda), qui est fonction de lambda, suivant la relation :




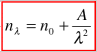
D'où provient cette formule et comment est calculé A ?

Tout d'abord introduisons le nombre d'Abbe, Vd, obtenu par la formule :

Vd=constante propre à chaque matériau ( Vd= 64.2 par exemple pour le BK7, Nd = 1.1517 ).
NF=indice de réfraction pour la lumière bleue, avec LambdaF=486.13 nm
NC=indice de réfraction pour la lumière rouge, avec LambdaC=656.27 nm
Nd=indice de réfraction pour la lumière jaune, avec Lambdad=587.56 nm
Le matériel optique est caractérisé par Vd et Lambdad.

Les valeurs de A et No sont déduites des formules :


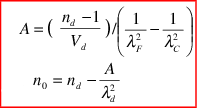
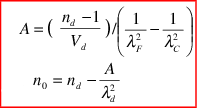
L'important sur ce phénomène de dispersion est donc de retenir que l'indice du milieu va être légèrement modifié en fonction de la longueur d'onde de la lumière émise( et donc de sa couleur ). C'est pourquoi le rayon réfracté va être légèrement modifié quand la source lumineuse varie.
Le rayon incident garde la même direction, défnie par Ai angle incident.